Fundamentals of Microelectronics

Last updated Mar 18, 2023

# Need for Current Mirrors in Microelectronics

• The biasing provided to circuits should be independent of:

  • Voltage variation: Eg, the voltage from a battery drops as it discharges slowly
  • Temperature variation: Eg, different environments / places have different ambient temperatures

• How does temperature affect the operation of circuits?

  • 
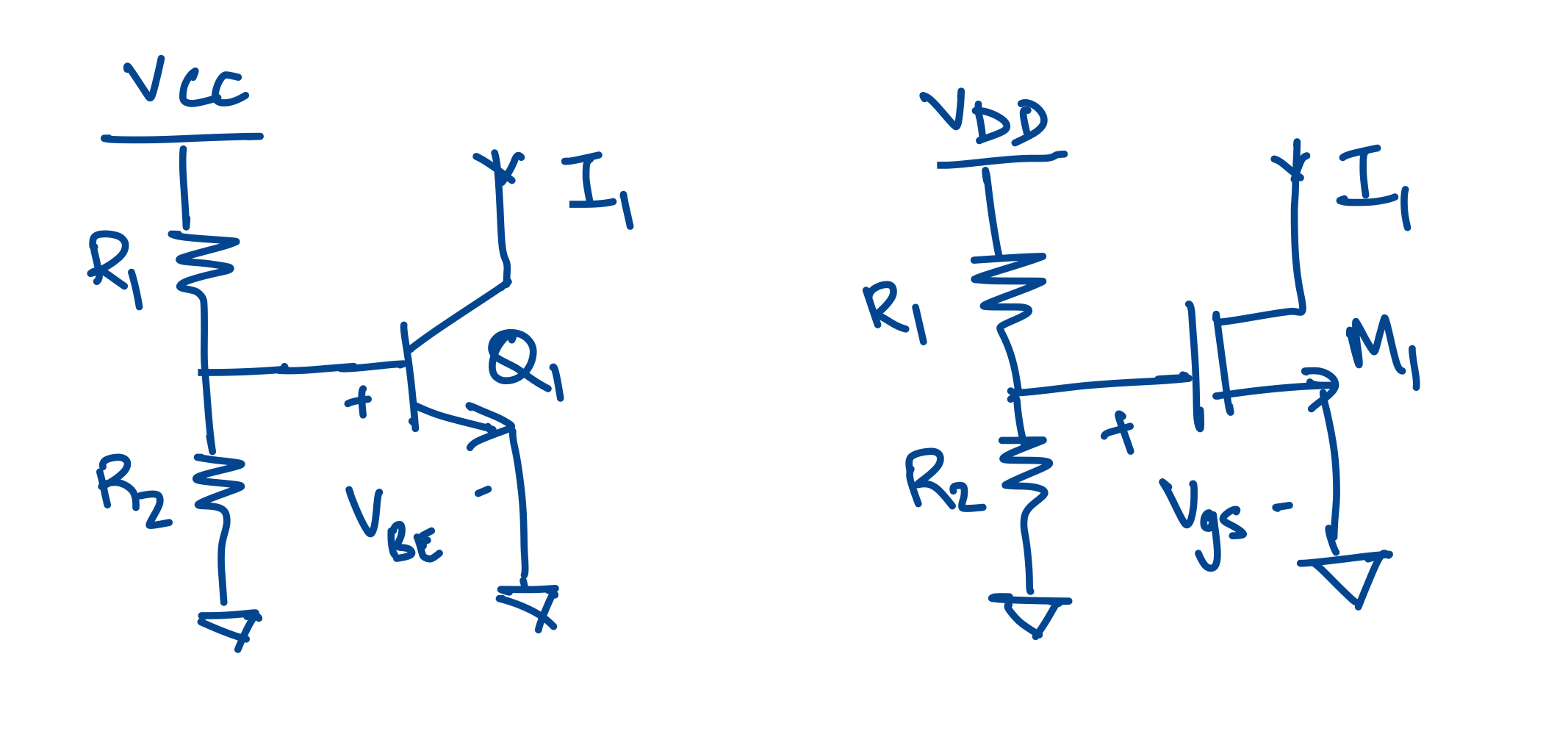
  • BJT example
    • For a desired current $I_1$,
      • $$ \frac{R_2}{R_1+R_2}V_{cc}=V_T ln\frac{I_1}{I_S} $$
    • even if resistors are made of same material, and vary the same amount, $V_T$ and $I_S$ vary with temperature, resulting in varying current $I_1$
  • FET example
    • For a desired current $I_1$
      • $$ I_1= \frac{1}{2}\mu_nC_{ox}(\frac{R_2}{R_1+R_2}V_{DD}-V_{TH})^2 $$
    • Even if resistors vary the same amount, mobility $\mu_n$ and threshold voltage $V_{TH}$ vary with temperature resulting in varying current $I_1$

• It is possible to design a circuit called Band Gap Reference that can provide voltage- and temperature independent voltage and currents, but this uses 10’s of transistors and is fairly complex.

• The idea is to generate a golden reference current (or voltage) from a Band Gap Reference circuit, and merely “copy” that reference current to wherever it is needed in the whole circuit. The circuit that does the copying is called a current mirror

# Working principle of a Current Mirror

The basic idea is to use the current generated from a golden source like a bandgap reference circuit and use that to generate a voltage, which will then be applied to another transistor to generate a copy of the current.

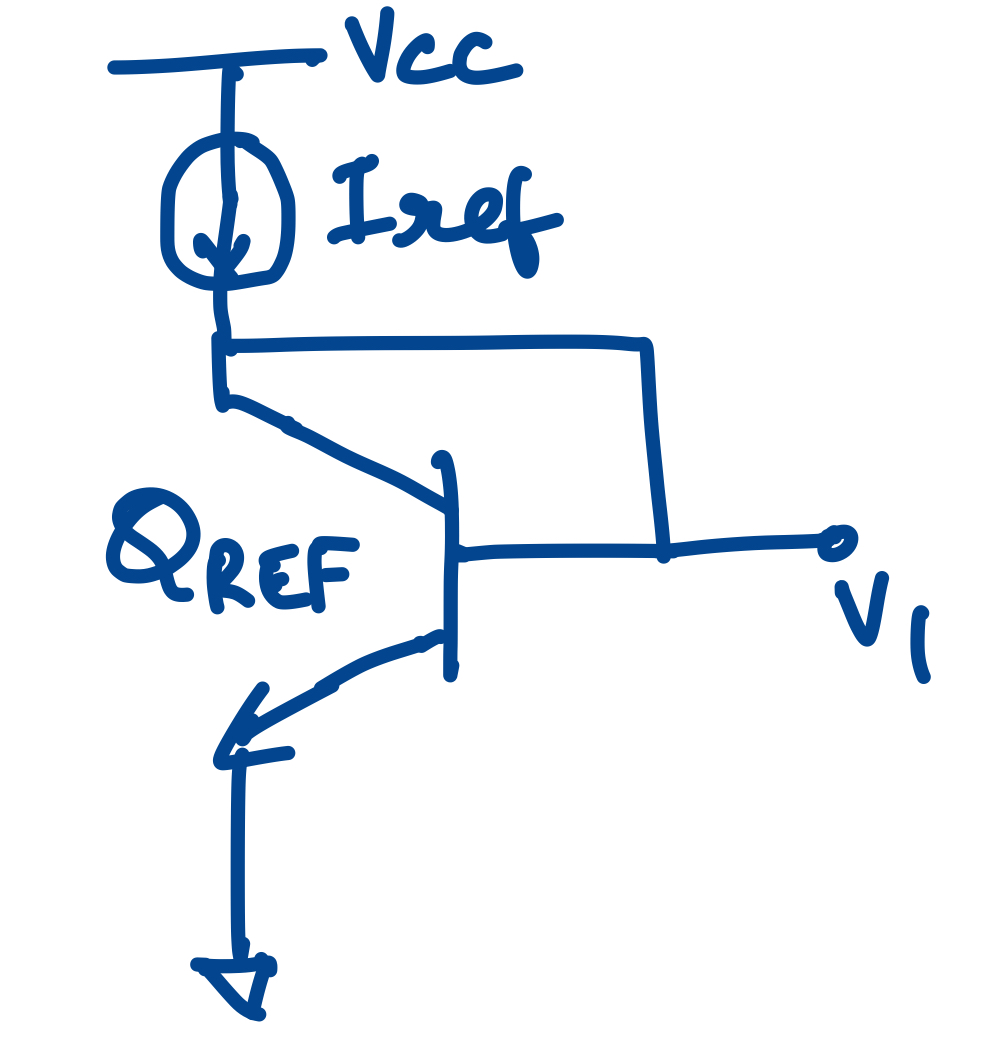
A diode connected bipolar transistor does exactly this. The relationship of voltage $V_1$ to the current $I_{ref}$ is $$ V_1 = V_Tln\frac{I_{REF}}{I_{S,REF}} $$ where $I_{S,REF}$ is the saturation current of the reference transistor.

Let us construct the whole current source now.

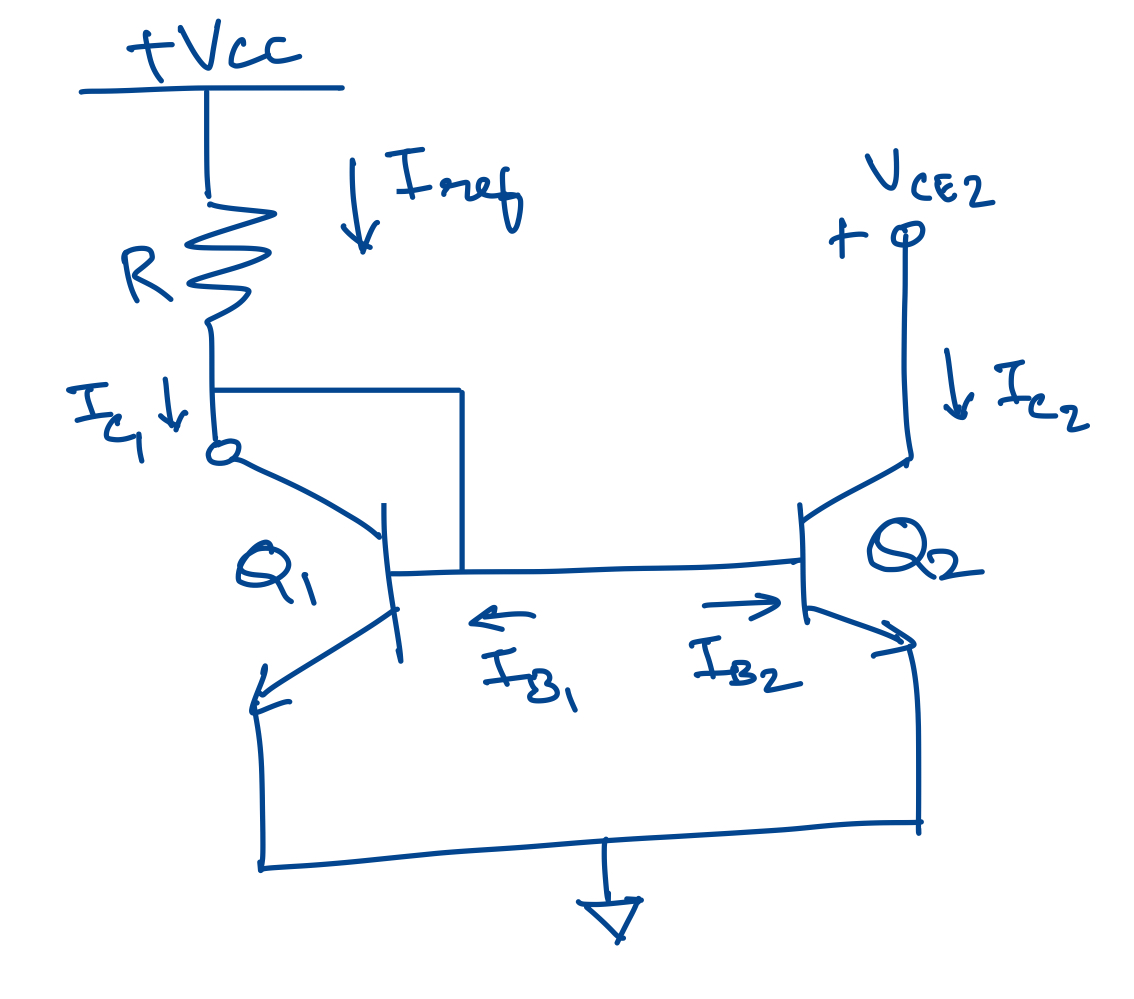
The voltage at the base of transistors Q1 and Q2 is proportional to the natural logarithm of the reference current from the bandgap reference circuit, and is a result of the diode connected transistor Q1. Transistor Q2 takes the voltage at its base and creates a “copy” or “mirrors” the current to the output side, provided transistors Q1 and Q2 are identical to each other, or some integer multiple thereof.

So, how does this solve the temperature sensitivity issue? The voltage at the base of the transistors does vary with temperature. But since Q1 and Q2 are identical, they are affected in the same way by temperature. As a result, the copied current is insensitive to temperature.

# Using a current mirror to create multiple copies, multiples, or fractions of a reference current

• Once the $V_{BE}$ voltage has been generated from the reference current (that uses bandgap reference) using the diode connected transistor, it can be used as the $V_{BE}$ for several output transistors.
  • If you apply the voltage to several transistors Q3, Q4, Q5, then you can create 3 copies of the reference current.
  • If you apply the voltage to several transistors Q3, Q4, Q5 and then tie their collectors together, you can create one 3X copy of the reference current
  • If you size the reference transistor to be 3 parallel transistors, and have only one output transistor, you can generate fractional 1/3 current copies.
  • If you have a reference transistor of size 3X, and output transistors of size 1X and 12X, you can generate both multiplier and fractional current copies (1/3rd and 4X in this case)

• Behzad Razavi, Fundamentals of Microelectronics, 2013, Wiley, Chapter 9