deriving expressions for transit frequency of a MOSFET
Consider the small signal equivalent circuit of a MOSFET shown below. We assume here that $V_{BS}=0$, so there are no body currents flowing in the device.
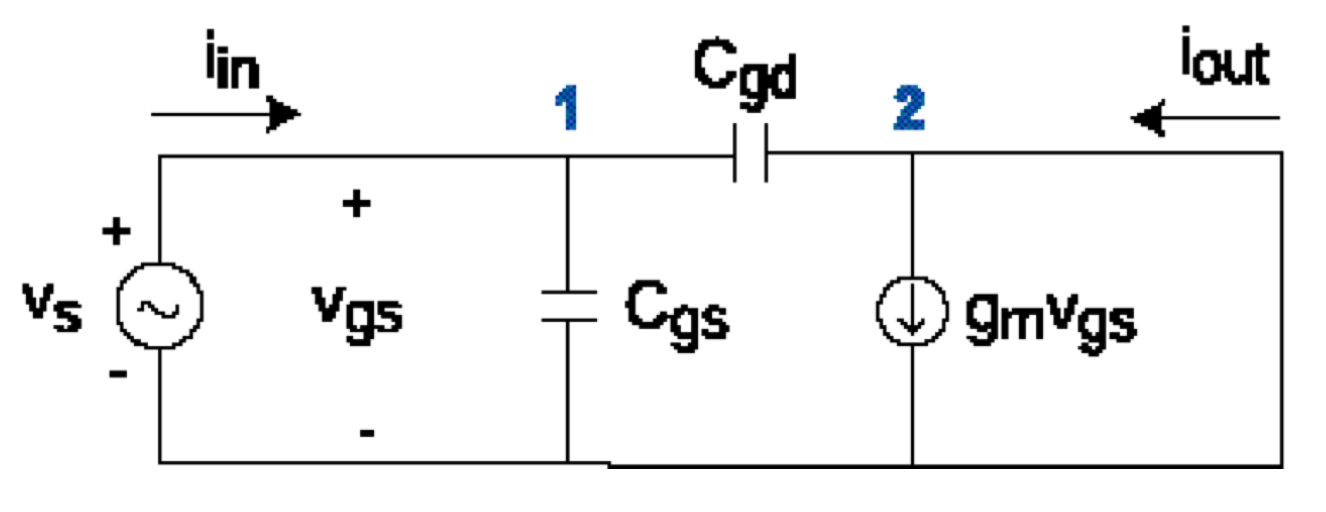
Writing KCL at Node 1: $$ I_{in}-j\omega C_{gs}V_{gs} - j\omega C_{gd}V_{gs} = 0, $$ $$ I_{in}=j\omega(C_{gs}+C_{gd})V_{gs} $$ Writing KCL at Node 2: $$ I_{out}+j\omega C_{gd}V_{gs}-g_mV_{gs}=0, $$ $$ I_{out}=(g_m-j\omega C_{gd})V_{gs} $$ Something to note at Node 2, is that current is flowing from the input side into Node 2 through Cgd, combining with $I_{out}$ and leaving as $g_mV_{gs}$ . Looking at it this way should explain the signs of current.
Current gain is now easy to calculate, $$ h_{21}= I_{out}/I_{in} = \frac{g_m-j\omega C_{gd}}{j\omega(C_{gs}+C_{gd})} $$ and magnitude of $h_{21}$ is, $$ |h_{21}|=\frac{\sqrt{g_m^2+\omega^2C_{gd}^2}}{\omega(C_{gs}+C_{gd})} $$